Are you ready to embark on a journey to learn the mathematics needed for machine learning and data science? Look no further! In this blog, I have compiled a list of topics in mathematics that will help you get started on your path to mastering machine learning and data science. Learning theory can be challenging and tedious, especially when it comes to mathematics, and many of us have disliked it in the past. But remember, to achieve greatness, we must overcome our challenges and push through the discomfort. If you want to master machine learning or data science, you must have a basic understanding of the topics mentioned below. So, even if you find it difficult, stay committed and learn these topics to take your skills to the next level. Without further ado, here are the topics you should learn to become a master of machine learning and data science.

1. Algebra
Algebra is a branch of mathematics that involves solving mathematical expressions represented by symbols.
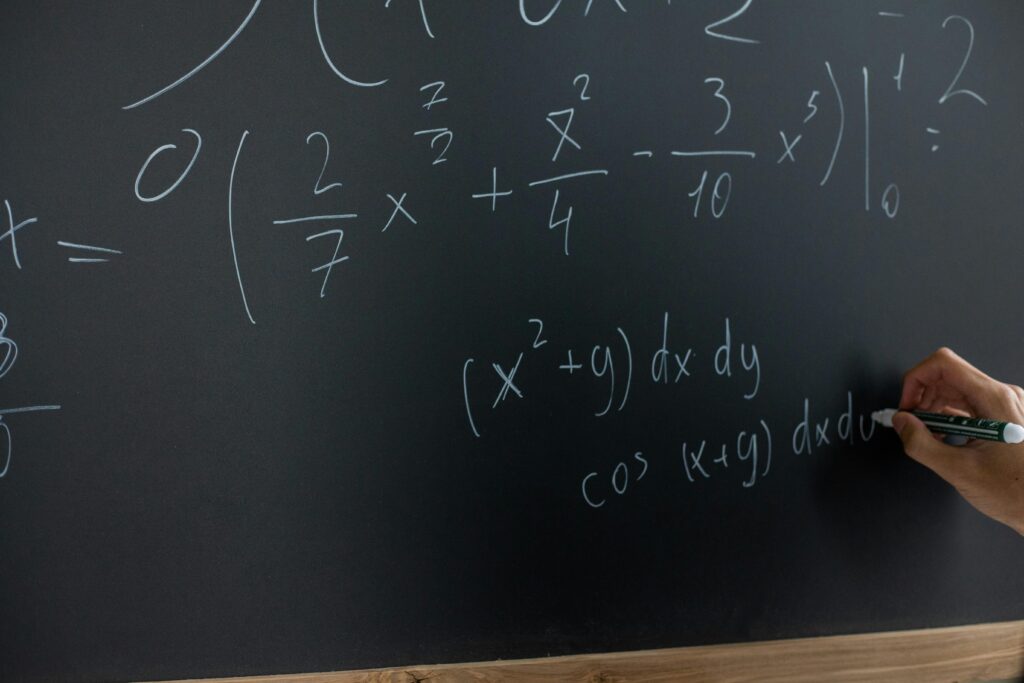
Are you looking to master algebra? Then pay attention to these essential topics: exponents, radicals, factorials, summations, and scientific notations. By focusing on these concepts, you’ll build a strong foundation for advanced mathematics and scientific applications. Don’t miss out on the chance to become a true algebra expert. Invest in your education and start mastering these topics today!
2. Linear Algebra
Linear algebra is a field of mathematics that concentrates on understanding vectors, vector spaces, linear transformations, and systems of linear equations. It involves examining and modifying linear relationships between variables, frequently using matrices and their operations.

Important topics in linear algebra include scalars, vectors, matrices, tensors, eigenvectors, eigenvalues, singular value decomposition, principal component analysis (PCA), and dot, vector, and Hadamard products. Mastery of these concepts is essential for success in fields such as mathematics, physics, engineering, computer science, and data analysis.
3. Calculus
Calculus is an essential area of study that plays a vital role in solving real-world problems. It provides a powerful framework for understanding and modeling the world around us, allowing us to analyze rates of change and accumulation. Whether you aspire to be an engineer, scientist, or mathematician, mastering calculus will set you on the path to success.
In simple terms, Calculus is the math of change and motion, focusing on rates of change (differential calculus) and accumulation (integral calculus).
When it comes to calculus, there’s no need to be intimidated. With confidence and determination, you can master these essential topics and gain a competitive edge. Start by exploring the basics of functions, a fundamental concept that provides the foundation for more advanced calculus concepts. From there, dive headfirst into the exciting world of gradients, including the concept, intuition, properties, and directional derivative. Don’t stop there – explore the intricacies of derivatives, including rules such as addition, product, and chain rule, as well as hyperbolic derivatives like tanh and cosh, and partial derivatives. To truly become a calculus expert, you must also master vector and matrix calculus, including different derivative operators such as Gradient, Jacobian, Hessian, and Laplacian. Finally, explore gradient algorithms to gain a competitive edge, including topics such as local and global maxima and minima, saddle points, convex functions, batches and mini-batches, stochastic gradient descent, and performance comparison. With a confident and determined mindset, you can conquer these essential calculus topics and become a true expert. So what are you waiting for? Start exploring today!
4. Statistics & Probability
Understanding the difference between statistics and probability is crucial to making informed decisions in today’s data-driven world. Statistics is the key to unlocking insights from vast amounts of data, allowing us to make informed decisions based on evidence. Probability, on the other hand, helps us to understand the likelihood of different outcomes, enabling us to make informed predictions and take calculated risks. By mastering these two essential concepts, we can gain a deeper understanding of the world around us and make more informed decisions.
In simple terms, Statistics is decoding data for insights, while probability is gauging the likelihood of events.
These are the topics that we will be discussing in statistics and probability:
– Basic Statistics: This includes mean, median, mode, variance, covariance, and other related concepts.
– Basic Rules in Probability: In probability, we will explore events, dependent and independent events, sample spaces, frequentist approach, and conditional probability.
– Random Variables: We will discuss continuous and discrete random variables, expectation, variance, joint and conditional distributions.
– Bayes’ Theorem: This theorem calculates the validity of beliefs and helps machines recognize patterns and make decisions. Bayesian software is used for this purpose.
– Maximum Likelihood Estimation (MLE): This is a method used for parameter estimation. It requires knowledge of fundamental probability concepts such as joint probability and independence of events.
– MAP (Maximum a posteriori estimation): This is another method used for parameter estimation.
– Common Distributions: Finally, we will cover common distributions such as binomial, Poisson, Bernoulli, Gaussian, exponential, and Conjugate priors.
5. Information Theory
Information theory can be thought of as the language of communication. It involves the study of how information is encoded, transmitted, and decoded across different channels both efficiently and reliably. It is the art and science of quantifying information, measuring its entropy, and finding ways to compress and transmit it while minimizing errors. Information theory is crucial in modern communication systems, from digital technology to genetics, as it guides us in maximizing the flow of information while minimizing noise and uncertainty.

Information theory is a fascinating topic that plays a crucial role in our everyday lives. Understanding key concepts such as entropy, cross-entropy, Kullback Leibler Divergence, the Viterbi Algorithm, Encoder-Decoder, mutual information, and Markov Chain can open doors to exciting opportunities in fields such as Natural Language Processing (NLP), Speech, and Machine Translation RNNs. So, don’t hesitate to dive into these concepts, learn them inside out, and see where it takes you. You’ll be amazed at the possibilities that await you!
Are you ready to unlock the full potential of cutting-edge technologies that are shaping our world? Look no further than mathematics for machine learning and data science specialization. It’s the key to endless possibilities. By immersing yourself in the foundational principles of mathematics, you’ll equip yourself with the necessary tools to succeed in this exciting field. But don’t stop there. Keep exploring and stay up-to-date by visiting my blog website regularly. It’s filled with detailed breakdowns of mathematical concepts and their practical applications in machine learning and data science. With every visit, you’ll discover something new, expand your knowledge and skills, and be one step closer to achieving your goals. So don’t hesitate. Join me on this journey of learning and discovery and let’s unlock the full potential of mathematics together!
